TripleA Turn Summary for game: Europe Improved
Game History
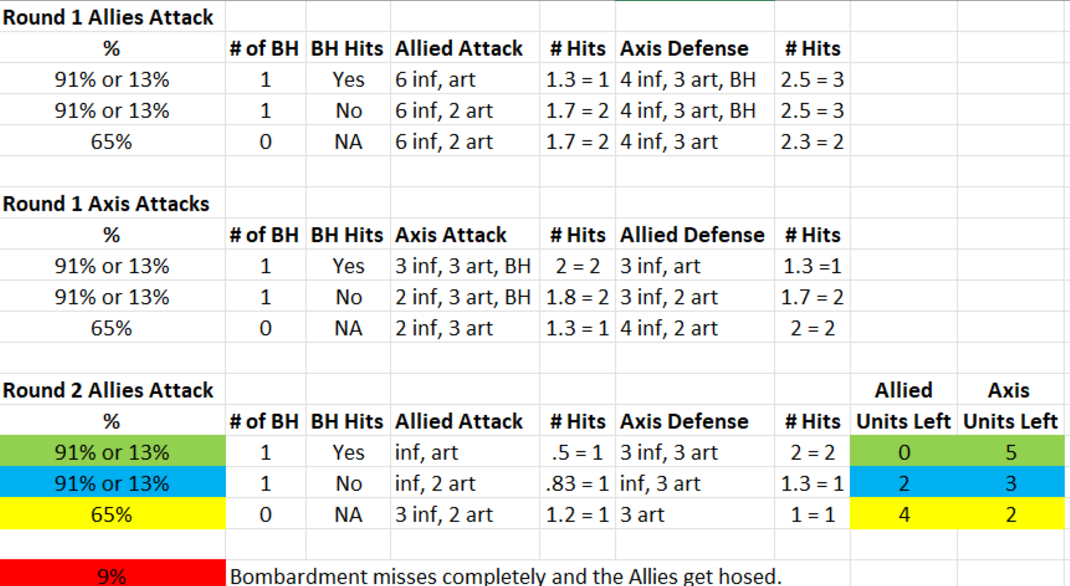
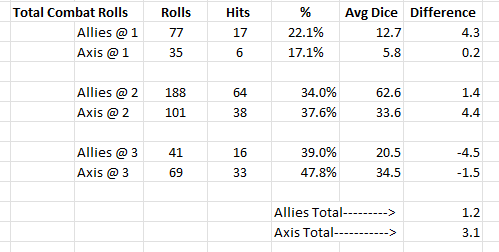
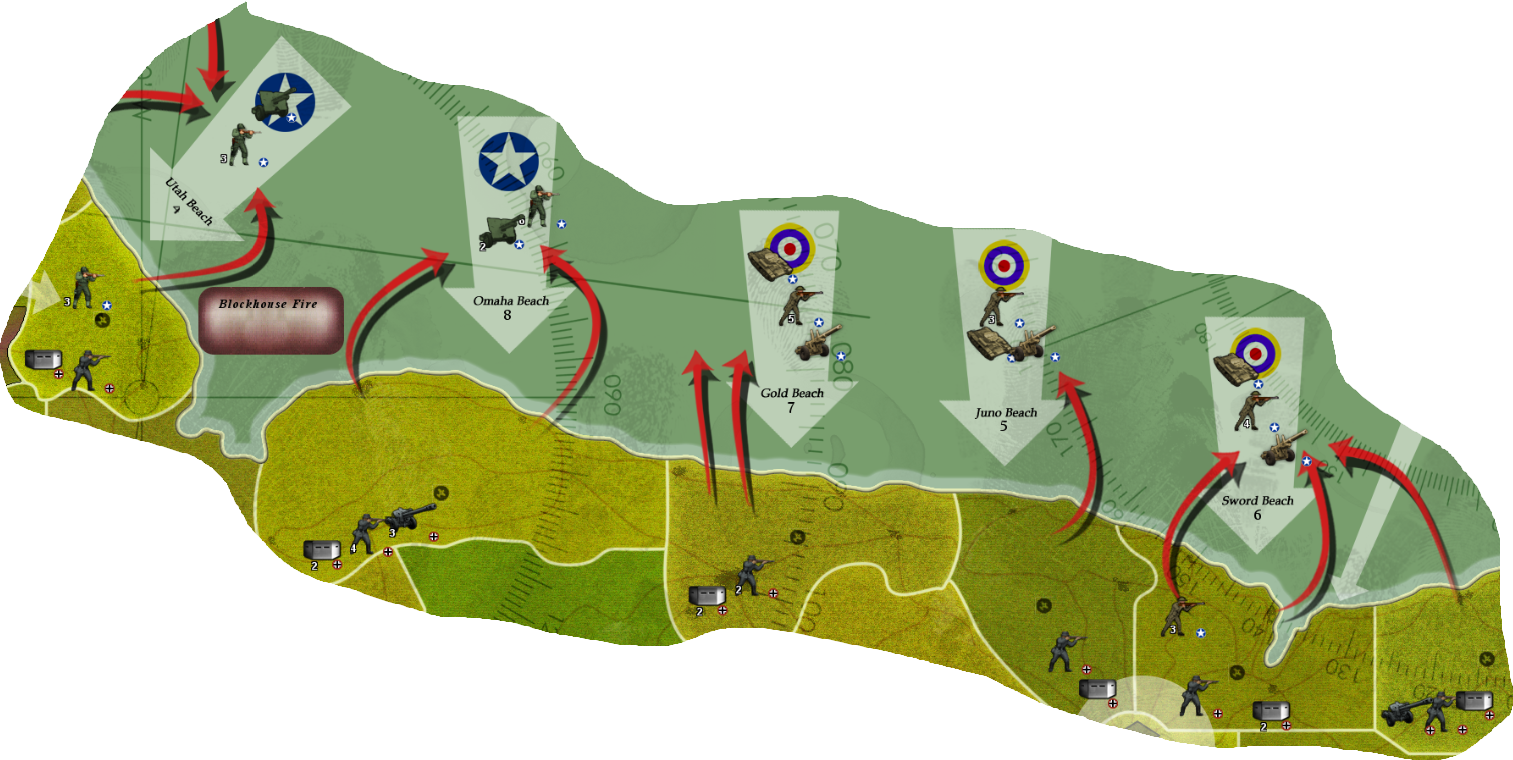
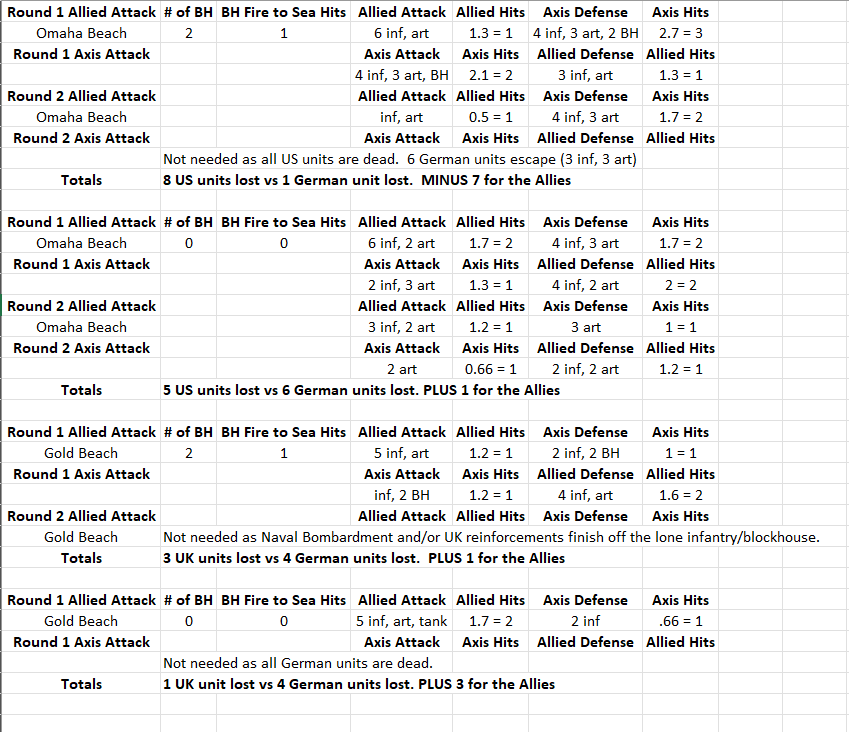
Round: 1 Purchase Units - Germans Germans buy 13 infantry; Remaining resources: 1 PUs; Combat Move - Germans Turning on Edit Mode EDIT: Removing units owned by Germans from Bay of Biscay Sea Zone: 1 submarine EDIT: Removing units owned by Germans from Rumania: 1 infantry EDIT: Turning off Edit Mode 1 submarine moved from Denmark Strait Sea Zone to British Convoy 4 Sea Zone Germans take British Convoy 4 Sea Zone from British 1 submarine moved from British Convoy 4 Sea Zone to Davis Strait Sea Zone 1 submarine moved from Halifax Sea Sea Zone to Davis Strait Sea Zone 1 submarine moved from Mid-Atlantic Sea Zone to Davis Strait Sea Zone 1 submarine moved from Azores Sea Sea Zone to British Convoy 3 Sea Zone Germans take British Convoy 3 Sea Zone from British 1 submarine moved from British Convoy 3 Sea Zone to Celtic Sea Sea Zone 1 submarine moved from South Atlantic Sea Zone to Celtic Sea Sea Zone 1 submarine moved from Bay of Biscay Sea Zone to Celtic Sea Sea Zone 1 submarine moved from Danish Sea Sea Zone to English Channel Sea Zone 1 submarine and 1 transport moved from Danish Sea Sea Zone to North Sea Sea Zone 1 submarine moved from Barents Sea Sea Zone to North Sea Sea Zone 1 bomber moved from Germany to Celtic Sea Sea Zone 1 fighter moved from France to Celtic Sea Sea Zone 1 fighter moved from Northern Italy to English Channel Sea Zone 1 fighter moved from Norway to North Sea Sea Zone 2 fighters moved from Germany to North Sea Sea Zone 1 artillery and 3 infantry moved from Hungary to Bessarabia 1 fighter moved from Poland to East Poland 1 artillery and 5 infantry moved from Poland to East Poland 1 battleship and 1 destroyer moved from Tyrrhenian Sea Sea Zone to Strait of Gibraltar Sea Zone Combat - Germans Battle in Davis Strait Sea Zone Germans attack with 3 submarines British defend with 1 destroyer and 1 transport Germans roll dice for 3 submarines in Davis Strait Sea Zone, round 2 : 1/3 hits, 1,00 expected hits British roll dice for 1 destroyer and 1 transport in Davis Strait Sea Zone, round 2 : 0/2 hits, 0,67 expected hits 1 transport owned by the British lost in Davis Strait Sea Zone Germans roll dice for 3 submarines in Davis Strait Sea Zone, round 3 : 0/3 hits, 1,00 expected hits British roll dice for 1 destroyer in Davis Strait Sea Zone, round 3 : 0/1 hits, 0,50 expected hits Germans roll dice for 3 submarines in Davis Strait Sea Zone, round 4 : 0/3 hits, 1,00 expected hits British roll dice for 1 destroyer in Davis Strait Sea Zone, round 4 : 1/1 hits, 0,50 expected hits 1 submarine owned by the Germans lost in Davis Strait Sea Zone Germans roll dice for 2 submarines in Davis Strait Sea Zone, round 5 : 1/2 hits, 0,67 expected hits British roll dice for 1 destroyer in Davis Strait Sea Zone, round 5 : 0/1 hits, 0,50 expected hits 1 destroyer owned by the British lost in Davis Strait Sea Zone Germans win with 2 submarines remaining. Battle score for attacker is 12 Casualties for British: 1 destroyer and 1 transport Casualties for Germans: 1 submarine Battle in Celtic Sea Sea Zone Germans attack with 1 bomber, 1 fighter and 3 submarines British defend with 1 destroyer and 2 transports Germans roll dice for 3 submarines in Celtic Sea Sea Zone, round 2 : 1/3 hits, 1,00 expected hits Germans roll dice for 1 bomber and 1 fighter in Celtic Sea Sea Zone, round 2 : 2/2 hits, 1,17 expected hits British roll dice for 1 destroyer and 2 transports in Celtic Sea Sea Zone, round 2 : 2/3 hits, 0,83 expected hits 2 submarines owned by the Germans lost in Celtic Sea Sea Zone 1 destroyer owned by the British and 2 transports owned by the British lost in Celtic Sea Sea Zone Germans win with 1 bomber, 1 fighter and 1 submarine remaining. Battle score for attacker is 12 Casualties for Germans: 2 submarines Casualties for British: 1 destroyer and 2 transports Battle in Bessarabia Germans attack with 1 artillery and 3 infantry Russians defend with 1 armour and 1 infantry Germans roll dice for 1 artillery and 3 infantry in Bessarabia, round 2 : 0/4 hits, 1,00 expected hits Russians roll dice for 1 armour and 1 infantry in Bessarabia, round 2 : 1/2 hits, 0,67 expected hits 1 infantry owned by the Germans lost in Bessarabia Germans roll dice for 1 artillery and 2 infantry in Bessarabia, round 3 : 0/3 hits, 0,83 expected hits Russians roll dice for 1 armour and 1 infantry in Bessarabia, round 3 : 0/2 hits, 0,67 expected hits Germans roll dice for 1 artillery and 2 infantry in Bessarabia, round 4 : 0/3 hits, 0,83 expected hits Russians roll dice for 1 armour and 1 infantry in Bessarabia, round 4 : 1/2 hits, 0,67 expected hits 1 infantry owned by the Germans lost in Bessarabia Germans roll dice for 1 artillery and 1 infantry in Bessarabia, round 5 : 0/2 hits, 0,67 expected hits Russians roll dice for 1 armour and 1 infantry in Bessarabia, round 5 : 0/2 hits, 0,67 expected hits Germans roll dice for 1 artillery and 1 infantry in Bessarabia, round 6 : 0/2 hits, 0,67 expected hits Russians roll dice for 1 armour and 1 infantry in Bessarabia, round 6 : 0/2 hits, 0,67 expected hits Germans roll dice for 1 artillery and 1 infantry in Bessarabia, round 7 : 2/2 hits, 0,67 expected hits Russians roll dice for 1 armour and 1 infantry in Bessarabia, round 7 : 0/2 hits, 0,67 expected hits 1 infantry owned by the Russians and 1 armour owned by the Russians lost in Bessarabia Germans win, taking Bessarabia from Russians with 1 artillery and 1 infantry remaining. Battle score for attacker is 2 Casualties for Germans: 2 infantry Casualties for Russians: 1 armour and 1 infantry Battle in East Poland Germans attack with 1 artillery, 1 fighter and 5 infantry Russians defend with 4 infantry Germans roll dice for 1 artillery, 1 fighter and 5 infantry in East Poland, round 2 : 0/7 hits, 1,83 expected hits Russians roll dice for 4 infantry in East Poland, round 2 : 0/4 hits, 1,33 expected hits Germans roll dice for 1 artillery, 1 fighter and 5 infantry in East Poland, round 3 : 2/7 hits, 1,83 expected hits Russians roll dice for 4 infantry in East Poland, round 3 : 2/4 hits, 1,33 expected hits 2 infantry owned by the Germans lost in East Poland 2 infantry owned by the Russians lost in East Poland 1 fighter owned by the Germans retreated 1 artillery owned by the Germans and 3 infantry owned by the Germans retreated to Poland Russians win with 2 infantry remaining. Battle score for attacker is 0 Casualties for Germans: 2 infantry Casualties for Russians: 2 infantry Battle in North Sea Sea Zone Germans attack with 3 fighters, 2 submarines and 1 transport British defend with 1 battleship, 1 destroyer and 1 transport Germans roll dice for 2 submarines in North Sea Sea Zone, round 2 : 0/2 hits, 0,67 expected hits Germans roll dice for 3 fighters and 1 transport in North Sea Sea Zone, round 2 : 2/3 hits, 1,50 expected hits Units damaged: 1 battleship owned by the British British roll dice for 1 battleship, 1 destroyer and 1 transport in North Sea Sea Zone, round 2 : 1/3 hits, 1,33 expected hits 1 transport owned by the Germans lost in North Sea Sea Zone 1 transport owned by the British lost in North Sea Sea Zone Germans roll dice for 2 submarines in North Sea Sea Zone, round 3 : 2/2 hits, 0,67 expected hits British roll dice for 1 battleship and 1 destroyer in North Sea Sea Zone, round 3 : 1/2 hits, 1,17 expected hits 1 submarine owned by the Germans lost in North Sea Sea Zone 1 destroyer owned by the British and 1 battleship owned by the British lost in North Sea Sea Zone Germans win with 3 fighters and 1 submarine remaining. Battle score for attacker is 28 Casualties for Germans: 1 submarine and 1 transport Casualties for British: 1 battleship, 1 destroyer and 1 transport Battle in Strait of Gibraltar Sea Zone Germans attack with 1 battleship and 1 destroyer British defend with 1 destroyer Germans roll dice for 1 battleship and 1 destroyer in Strait of Gibraltar Sea Zone, round 2 : 1/2 hits, 1,17 expected hits British roll dice for 1 destroyer in Strait of Gibraltar Sea Zone, round 2 : 0/1 hits, 0,50 expected hits 1 destroyer owned by the British lost in Strait of Gibraltar Sea Zone Germans win with 1 battleship and 1 destroyer remaining. Battle score for attacker is 12 Casualties for British: 1 destroyer Battle in English Channel Sea Zone Germans attack with 1 fighter and 1 submarine British defend with 1 destroyer Germans roll dice for 1 submarine in English Channel Sea Zone, round 2 : 1/1 hits, 0,33 expected hits British roll dice for 1 destroyer in English Channel Sea Zone, round 2 : 1/1 hits, 0,50 expected hits 1 submarine owned by the Germans lost in English Channel Sea Zone 1 destroyer owned by the British lost in English Channel Sea Zone Germans win with 1 fighter remaining. Battle score for attacker is 4 Casualties for Germans: 1 submarine Casualties for British: 1 destroyer Non Combat Move - Germans 2 artilleries and 4 infantry moved from Germany to Poland 2 infantry moved from Yugoslavia to Hungary 1 artillery and 1 infantry moved from Czechoslovakia to Poland 1 artillery and 1 infantry moved from Austria to Hungary 1 armour and 2 infantry moved from Rumania to Hungary 2 infantry moved from Bulgaria to Rumania 1 artillery and 2 infantry moved from Greece to Yugoslavia 2 armour moved from Northern Italy to Hungary 1 artillery moved from Northern Italy to Yugoslavia 1 infantry moved from Northern Italy to Yugoslavia 2 infantry moved from Southern Italy to Northern Italy 1 aaGun moved from Northern Italy to Austria 1 aaGun moved from Germany to Poland 2 armour moved from Germany to Poland 2 armour moved from Netherlands-Belgium to Poland 3 infantry moved from Netherlands-Belgium to Germany 4 infantry moved from Eastern France to Germany 2 armour moved from France to Germany 1 artillery and 4 infantry moved from France to Netherlands-Belgium 4 infantry moved from Norway to Finland 2 fighters moved from North Sea Sea Zone to Finland 1 fighter moved from North Sea Sea Zone to Germany 1 fighter moved from English Channel Sea Zone to Netherlands-Belgium 1 fighter moved from Celtic Sea Sea Zone to Netherlands-Belgium 1 bomber moved from Celtic Sea Sea Zone to Germany 1 fighter moved from East Poland to Germany 1 transport moved from Tyrrhenian Sea Sea Zone to Strait of Gibraltar Sea Zone 1 armour, 1 artillery and 1 infantry moved from Tunisia to Algeria 1 infantry moved from Morocco to Algeria 1 infantry moved from Denmark to Germany Place Units - Germans 13 infantry placed in Germany Turn Complete - Germans Germans collect 40 PUs; end with 41 PUsCombat Hit Differential Summary :
Russians regular : -2,67 Germans regular : -3,50 British regular : -0,50